D2L Chapter 6-7 Note

Interpretation of Conv2d layers

nn.Conv2d(6, 16, kernel_size=5):

• There are 16 filters, each of them will generate a channel, resulting a total of 16 channels in output
• Each those 16 filters has 6 layers
• Each layer operates on one of the 6 channels from input
• Each layer is of size (5, 5)
• Each filter is of shape (6, 5, 5)
• For each of those 16 filters, after convoluting on 6 channels, the reuslts are added together to get only 1 channel of new features. Since there are 16 filters, the output has 16 channels.

Batchnorm

• Why
  • For very deep networks, gradients are tend to vanish or explode
  • “Internal covariate shift”: the distribution of inputs to each layer changes as the params from previous layer change
• What To stable the params during training process, and subsequently stable gradients
• How
  • Standardize the batch input, use 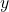as the input for next layer:
    • 
    • 
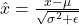
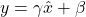
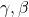    • are learnable params

Fancier CNNs

• AlexNet
  • Features in images can be learned by model itself, and the model train itself based on those learned features
    • Earlier layers: Color, texture, …
    • Middle layers: Parts of objects, shape
    • Top layers: Objects, …
• VGG
  • Tie multiple conv2D and maxpool2D layers as one whole module, and reuse that module
  • A VGG block takes the number of conv2D layers and output channel and outputs a block that contains defined conv2D layers with a final layer of maxpool2D
  • VGG -> VGG -> … -> dense(4096) -> dense(4096) -> dense(1000)
• NiN
  • Still uses blocks as in VGG
  • In each block, two 1×1 conv2D layers are used, serving the purpose of final FC layers of the traditional CNN networks
  • NiN -> maxpool2D -> NiN -> maxpool2D -> … -> NiN -> Global average pooling layer
• GoogLeNet
  • Uses a block on steroid
  • Used 2 filters of different size to capture features in different perspectives
  • Used 1×1 conv2D layer to decrease number of channels
• ResNet
  • Incorporates the information from raw input of a block
  • y = f(x) + x
  • In this way:
    • Gradients can be back propagated with fewer steps in between, thus mitigating the effect of gradient vanishing or exploding. Essentially, gradients can take shortcuts to back propagate
    • Trained params are closer to theoretically perfect params: see this