RNN
Basic structure
- Hidden layer:
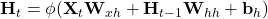
- X: (n, d), n is batch_size and d is dimension
- W_xh: (d, h): how to transform input
- H_t-1: (n, h): hidden layer from prev time step
- W_hh: (h, h): how to use hidden layer form prev time step
- b_h: (1, h): bias
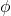 : Activation (ReLU, …)
: Activation (ReLU, …)
- Output layer:
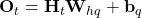
- H_t: (n, h)
- W_hq: (h, q)
- b_q: (1, q)
- O: (n, q): output logit, can use softmax(O) to get class probabilities
- Where
- n = batch_size
- d = input_dimension
- h = hidden_size
- q = output_features_size, basically how many things we want the model to spit out
How is it trained
- Perplexity
- It is a metric
- For a language model, it is the average number of guesses a model make about the next word, when the model is given a sentence
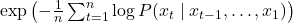 .
.
- Based on cross entropy
- example
- In best cases, those probabilities are all 1, and the perplexity would be
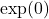 = 1
= 1 - In worst cases, those probabilities are infinitely small, the perplexity would be infinitely large
- In best cases, those probabilities are all 1, and the perplexity would be
- By the way some notes about cross entropy because I forget everything in 2 fucking seconds
- Entropy quantifies the “surprise” element of a thing, like the surprise of drawing a ssr
- Cross entropy’s cross part is “crossing over” tso another distribution
- This is used when we are comparing 2 distributions
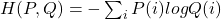 , where P is true distribution and Q is predicted distribution
, where P is true distribution and Q is predicted distribution- If P=Q, then H is just the entropy of P, the prediction progress created no added uncertainty
- If Q deviates from P, then this H will be larger than the entropy of P, and the larger the gap, the more problematic of (more uncertainty in) Q’s predicted distributions
- Back propagation through time
- See BPTT算法详解:深入探究循环神经网络(RNN)中的梯度计算【原理理解】-CSDN博客
- During this process, gradients are vulnerable to vanishing (when one or many gradients are small) or exploding (when one or many gradients are too large)
- Gradient clipping is used to address this issue. When a gradient is too big, scale that gradient down by some rules
Fancier RNNs
“ “
“
GRU
- Gated Recurrent Unit
- Gimmicks
- Reset gate
- A FC layer with Sigmoid activation function, thus value is only in [0, 1]
- For value of each cell:
- Approaches 0 -> the value of corresponding cell on
 should be reset
should be reset - Approaches 1 -> …… should not reset
- Approaches 0 -> the value of corresponding cell on
- The effect of resetting
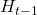 is manifested by using
is manifested by using 
- multiply whatever by a value close to 0 weakens its effect
- ….. close to 1 means almost no weakening of its effect
- Update gate
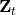
- A FC layer with Sigmoid activation function, thus value is only in [0, 1]
- For value of each cell:
- Approaches 0 -> More portion in
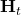 is from
is from 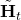
- Approaches 1 -> Less ……
- Approaches 0 -> More portion in
- Reset gate
- Process: Overall structure see this
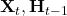 enters the unit and passes through Reset and Update gate
enters the unit and passes through Reset and Update gate
- In reset gate:
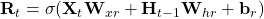
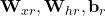 are params associated with Reset gate
are params associated with Reset gate
- In update gate:
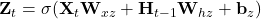
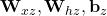 are params associated with Reset gate
are params associated with Reset gate
- In reset gate:
- Use
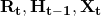 to generate candidate hidden state \tilde{\mathbf{H}}_t
to generate candidate hidden state \tilde{\mathbf{H}}_t
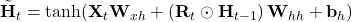 ,
,
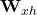 is used on
is used on 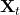
 operator enable the model to select which cell in
operator enable the model to select which cell in 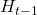 should be reset
should be reset- Activated using tanh because the value falls into [-1, 1]
- Use
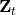 to calculate the final version of
to calculate the final version of 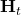
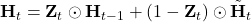 .
.- Basically, for each element, how much should be from
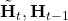 respectively
respectively
- One cell in
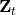 Approaches 0 -> More portion in
Approaches 0 -> More portion in 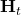 is from
is from 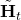
- One cell in
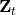 Approaches 1 -> Less ……
Approaches 1 -> Less ……
- One cell in
LSTM
- Long Short Term Memory
- GRU is a watered down version of this
- Gimmicks:
- Forget gate
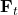
- FC layer with sigmoid activation
- Operates on the memories from prev step. Uses cell-wise multiplication (
 )
)
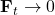 : More memories from the past (
: More memories from the past (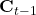 ) are forgotten
) are forgotten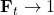 : … saved and used in the formation of new memories (
: … saved and used in the formation of new memories (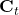 )
)
- Input gate
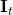
- FC layer with sigmoid activation
- Operates on candidate memory (
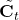 ) that is formed by tanh-ing the combination of
) that is formed by tanh-ing the combination of 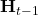 and
and 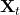
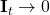 : More memories from candidate memory are forgotten
: More memories from candidate memory are forgotten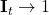 : … saved and used in the formation of new memories (
: … saved and used in the formation of new memories (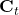 )
)
- Output gate
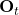
- FC layer with sigmoid activation
- Operates on the combined memory of
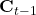 and
and 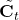 , which is to be the new memory,
, which is to be the new memory, 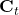
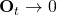 : Hidden cells will be updated more
: Hidden cells will be updated more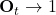 : Hidden cells will be updated less
: Hidden cells will be updated less
- Forget gate
- Process
- See flow chart in here
Encoder-Decoder & seq2seq
Steps of traditional seq2seq:
- Each word in a sentence get its embedding vector
- In each time step (for each word in a sentence), a h is generated and recorded
- The shape of h is dependent on the batch size and hidden size, for multiple layers, it is the output of the last layer. It has NOTHING TO DO with embedding size.
- in the final time step, the h generated in the final step is called “context vector” and is given a new letter c. For multiple layers, it is the hidden state of all layers.
- c acts as the initial hidden state (h_0) for the decoder and decoder use it to initiate the RNN
- For each output generated, it is fed as the x for the next RNN time step, until the output becomes , indicating the ending of a sentence
- The initial x is “<bos>”, indicating the beginning of a sentence
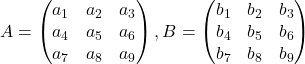
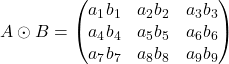
Comments are closed